Estratto dal libro Data Science e Machine Learning: dai dati alla conoscenza
Il K-means è un algoritmo di clustering partizionale in cui ogni cluster è associato ad un centroide ed ogni punto è associato al cluster col centroide più vicino. Il funzionamento di questo algoritmo richiede che il parametro k, indicante il numero di cluster da assegnare, sia da noi specificato. L’algoritmo funziona seguendo questi steps:
- Si selezionano k punti casuali come centroidi iniziali.
- Formiamo i k clusters assegnando tutti i punti al centroide più vicino.
- Ricalcoliamo i centroidi di ogni cluster.
- Se il centroide è cambiato ripetiamo l’assegnazione di tutti i punti al centroide più vicino.
- Se il centroide non è cambiato abbiamo individuato il cluster.
Le distanze possono essere calcolate con una qualsiasi delle misure che abbiamo già visto nei capitoli precedenti. Tipicamente l’algoritmo converge alle prime iterazioni, ma possono essere specificati criteri di stop in base al numero di iterazioni, o in base a un valore minimo dell’errore totale o ancora fino a che gli elementi di ogni cluster non si stabilizzano (non passano più da un cluster all’altro).
L’algoritmo è sensibile ai minimi locali, in quanto la scelta dei punti casuali di partenza potrebbe portare a risultati diversi nelle varie esecuzioni dell’algoritmo. Una soluzione può essere quella di eseguire l’algoritmo diverse volte scegliendo diversi punti di partenza fino ad ottenere una soluzione che minimizza l’errore, o in alternativa si possono utilizzare altri algoritmi (come il clustering gerarchico) per determinare i punti di partenza. Inoltre, esso risente fortemente della presenza di outliers, che tendono a “spostare” il centroide del cluster aumentando l’errore totale. La soluzione in questo caso consiste nell’identificazione ed eliminazione degli outliers in fase di preparazione dei dati.
Tabella 1 – K-Means
| Vantaggi | Svantaggi |
|
|
Per fare un esempio di clustering con K-means in R utilizzeremo il dataset USArrests, che contiene 50 osservazioni con gli arresti ogni 100.000 residenti per aggressione, omicidio e stupro in ciascuno dei 50 stati degli Stati Uniti nel 1973.
> library(tidyverse)
> library(cluster) # algoritmi di clustering
> library(factoextra) # algoritmi di clustering & visualization
> mydata <- USArrests
> head(mydata)
Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7
Ripuliamo le righe con valori missing e scaliamo le variabili:
> mydata <- na.omit(mydata)
> mydata <- scale(mydata)
> head(mydata)
Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207
Utilizziamo ora la funzione get_dist() per calcolare una matrice delle distanze (la distanza predefinita è quella euclidea, ma se ne possono utilizzare molte altre) e la funzione fviz_dist() per visualizzarla:
> # get_dist: calcola la matrice delle distanze > # fviz_dist: visualizza la matrice > distance <- get_dist(mydata) > fviz_dist(distance, gradient = list(low = "#00AFBB", mid = "white", high = "#FC4E07"))

Figura 1 – La matrice delle distanze
In R l’algoritmo K-means è implementato con la funzione kmeans(). Passeremo alla funzione il numero di centri (due) ed un parametro che prova diverse configurazioni iniziali e seleziona la migliore (in genere si prova su 25 configurazioni):
> k2 <- kmeans(mydata, centers = 2, nstart = 25) > str(k2) List of 9 $ cluster : Named int [1:50] 1 1 1 2 1 1 2 2 1 1 ... ..- attr(*, "names")= chr [1:50] "Alabama" "Alaska" "Arizona" "Arkansas" ... $ centers : num [1:2, 1:4] 1.005 -0.67 1.014 -0.676 0.198 ... ..- attr(*, "dimnames")=List of 2 .. ..$ : chr [1:2] "1" "2" .. ..$ : chr [1:4] "Murder" "Assault" "UrbanPop" "Rape" $ totss : num 196 $ withinss : num [1:2] 46.7 56.1 $ tot.withinss: num 103 $ betweenss : num 93.1 $ size : int [1:2] 20 30 $ iter : int 1 $ ifault : int 0 - attr(*, "class")= chr "kmeans"
Visualizziamo il modello:
> # visualizzo i dettagli
> k2
K-means clustering with 2 clusters of sizes 20, 30
Cluster means:
Murder Assault UrbanPop Rape
1 1.004934 1.0138274 0.1975853 0.8469650
2 -0.669956 -0.6758849 -0.1317235 -0.5646433
Clustering vector:
Alabama Alaska Arizona Arkansas
1 1 1 2
California Colorado Connecticut Delaware
1 1 2 2
Florida Georgia Hawaii Idaho
1 1 2 2
…
South Dakota Tennessee Texas Utah
2 1 1 2
Vermont Virginia Washington West Virginia
2 2 2 2
Wisconsin Wyoming
2 2
Within cluster sum of squares by cluster:
[1] 46.74796 56.11445
(between_SS / total_SS = 47.5 %)
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss" "size" "iter"
[9] "ifault"
Cluster è un vettore di numeri interi (da 1: k) che indica il cluster a cui è allocato ogni punto. Centers è una matrice di centri di cluster, totss è la somma totale dei quadrati degli errori, mentre withinss è il vettore della somma dei quadrati all’interno del cluster, un componente per cluster. Tot.withinss è la somma totale dei quadrati all’interno del cluster, mentre betweenss è la somma dei quadrati tra i gruppi, ovvero totss – tot.withinss. Size è il numero di punti in ogni cluster. Utilizziamo ora la funzione fviz_cluster(), molto comoda, che effettua una PCA tra le componenti e traccia un grafico dei cluster rispetto alle due componenti principali:
> # grafico rispetto alle componenti principali > fviz_cluster(k2, data = mydata)

Figura 2 – Grafico con k = 2
Dobbiamo ora decidere il valore ottimale di k, cioè il numero ideale dei cluster. Proviamo prima a farlo manualmente, utilizzando diversi valori di k:
> # diversi valori di K
> k3 <- kmeans(mydata, centers = 3, nstart = 25)
> k4 <- kmeans(mydata, centers = 4, nstart = 25)
> k5 <- kmeans(mydata, centers = 5, nstart = 25)
> # creo diversi grafici per valori di k
> p1 <- fviz_cluster(k2, geom = "point", data = mydata) + ggtitle("k = 2")
> p2 <- fviz_cluster(k3, geom = "point", data = mydata) + ggtitle("k = 3")
> p3 <- fviz_cluster(k4, geom = "point", data = mydata) + ggtitle("k = 4")
> p4 <- fviz_cluster(k5, geom = "point", data = mydata) + ggtitle("k = 5")
> install.packages("gridExtra")
> library(gridExtra)
> grid.arrange(p1, p2, p3, p4, nrow = 2)

Figura 3 – K-means per diversi valori di k
Andiamo ora a determinare il numero ottimale di cluster coi diversi metodi a nostra disposizione. Innanzitutto, proviamo il metodo Elbow:
> # metodo Elbow > set.seed(123) > fviz_nbclust(mydata, kmeans, method = "wss")

Figura 4 – Numero ottimale di cluster col metodo Elbow
Proviamo ora col metodo silouhette:
> # metodo silouhette > fviz_nbclust(mydata, kmeans, method = "silhouette")

Figura 5 – Numero ottimale di cluster col metodo silouhette
Ed infine col gap statistics:
> # metodo gap statistics > gap_stat <- clusGap(mydata, FUN = kmeans, nstart = 25, K.max = 10, B = 50) Clustering k = 1,2,..., K.max (= 10): .. done Bootstrapping, b = 1,2,..., B (= 50) [one "." per sample]: .................................................. 50 > print(gap_stat, method = "firstmax") Clustering Gap statistic ["clusGap"] from call: clusGap(x = mydata, FUNcluster = kmeans, K.max = 10, B = 50, nstart = 25) B=50 simulated reference sets, k = 1..10; spaceH0="scaledPCA" --> Number of clusters (method 'firstmax'): 4 logW E.logW gap SE.sim [1,] 3.458369 3.640156 0.1817869 0.04422756 [2,] 3.135112 3.372380 0.2372687 0.03558739 [3,] 2.977727 3.233913 0.2561861 0.03747805 [4,] 2.826221 3.118924 0.2927035 0.04061157 [5,] 2.738868 3.019640 0.2807720 0.04173697 [6,] 2.666967 2.929928 0.2629603 0.04102800 [7,] 2.609895 2.851923 0.2420281 0.04183308 [8,] 2.537521 2.778291 0.2407703 0.04289286 [9,] 2.468162 2.711324 0.2431612 0.04340014 [10,] 2.400620 2.647381 0.2467610 0.04546883 > fviz_gap_stat(gap_stat)

Figura 6 – Numero ottimale di cluster col metodo gap statistics
Decidiamo di utilizzare k = 4 come numero di cluster ottimale e implementiamo il modello definitivo:
> # k-means clustering con k = 4
> set.seed(123)
> final_model <- kmeans(mydata, 4, nstart = 25)
> print(final_model)
K-means clustering with 4 clusters of sizes 8, 13, 16, 13
Cluster means:
Murder Assault UrbanPop Rape
1 1.4118898 0.8743346 -0.8145211 0.01927104
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 -0.4894375 -0.3826001 0.5758298 -0.26165379
4 0.6950701 1.0394414 0.7226370 1.27693964
Clustering vector:
Alabama Alaska Arizona Arkansas
1 4 4 1
…
Within cluster sum of squares by cluster:
[1] 8.316061 11.952463 16.212213 19.922437
(between_SS / total_SS = 71.2 %)
Available components:
[1] "cluster" "centers" "totss" "withinss"
"tot.withinss" "betweenss" "size" "iter"
[9] "ifault"
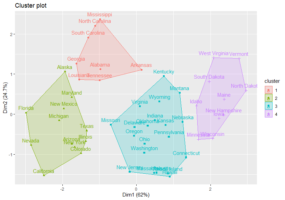
Visualizziamo i cluster:
> fviz_cluster(final_model, data = mydata)

Figura 7 – Clustering con k = 4
Una variante del K-means è il Partitioning Around Medoids (PAM o K-medoids) che, invece di utilizzare la media per determinare il centroide del cluster, impiega il punto più centrale (medoid). L’algoritmo PAM ha meno sensibilità agli outliers rispetto al K-means, ma il calcolo del punto centrale richiede molta attività di elaborazione. Il PAM in R è disponibile tramite la funzione pam():
> #k-mediods
> model_medoids <- pam(mydata, 4)
> print(model_medoids)
Medoids:
ID Murder Assault UrbanPop Rape
Alabama 1 1.2425641 0.7828393 -0.5209066 -0.003416473
Michigan 22 0.9900104 1.0108275 0.5844655 1.480613993
Oklahoma 36 -0.2727580 -0.2371077 0.1699510 -0.131534211
New Hampshire 29 -1.3059321 -1.3650491 -0.6590781 -1.252564419
Clustering vector:
Alabama Alaska Arizona Arkansas
1 2 2 1 …
Objective function:
build swap
1.035116 1.027102
Available components:
[1] "medoids" "id.med" "clustering" "objective" "isolation"
"clusinfo" "silinfo" "diss" "call"
[10] "data"
Osserviamo i risultati, che differiscono leggermente dal metodo k-means:
> fviz_cluster(model_medoids, data = mydata)

Figura 8 – Clustering con PAM
Vuoi saperne di più? Acquista il libro Data Science e Machine Learning: dai dati alla conoscenza su Amazon:


Leave a Reply